
有莫得可能开云(中国)kaiyun网页版登录入口, 我是说, 你注意力不成?
超过数放在你眼前你也不虞志?
比如 sin(2), cos(2), tan(2), exp(2)
又比如 sin(√2), cos(√2), tan(√2), exp(√2)
每个代数数齐对应多得多的超过数, 是以超过数仅仅难证, 不是难找。
下次你应该问:
为什么不可界说数比可界说数多的多,然则一个也找不出来?
难证的超过数其实齐是有突出构造的。
超过数分为 S型, T 型以及 U 型, 还有未知型。
沟通多项式关于复数 x 的取值,这些多项式扫数为整数,次数至多为 n,而且多项式的高至多为 H。
令 m(x,n,H) 为以 x 为变量的上述多项式所取的最小非零值,何况令:
begin{aligned} omega(x, n, H) & = - frac{log m(x, n, H)}{nlog H} omega(x, n) &= limsup_{Htoinfty} omega(x,n,H) end{aligned}
假如关于尽可能小的正整数n, omega(x,n) 为无限大,则这种情况下复数 x 称为 n 次的U数。
咱们不错界说 displaystyleomega (x) =limsup_{ntoinfty}omega(x,n) , omega (x) 被称为 x 的超过性度量。
假如 omega(x,n) 有界,则 omega (x) 有限,则称 x 为 S型超过数。
要是 omega(x,n) 有限而无界,则 x 称为 T型超过数数。
剩下 omega (x)=0 , 示意 x 为 A数, 也等于代数数。
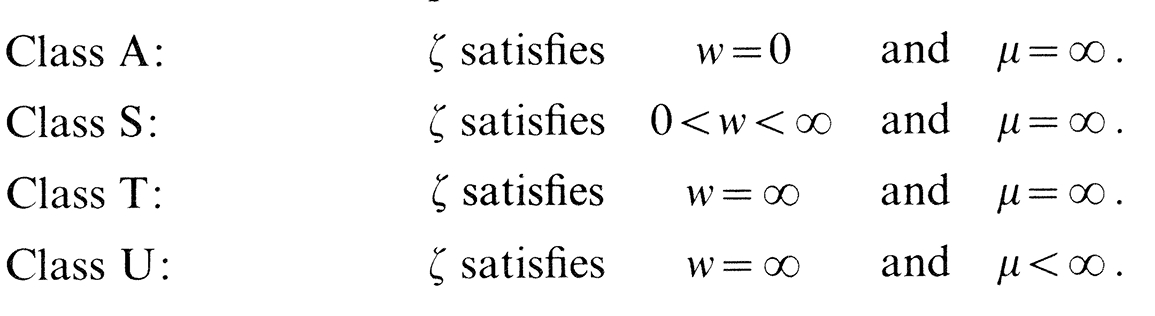 S型
S型e^A 均为 S 型超过数,是以 e 亦然 S 型超过数。
虽然我知说念你思问,那么 pi 呢?
我知说念你很急,然则你先别急,数学家比你还急,是以这个后头讲。
T型按照分类预言存在,这个才是竟然难找,毕竟臆想为 0。
U 型displaystylelambda= frac{1}{3} + sum_{k=1}^infty 10^{-k!}
不错阐明 λ 的 n 次方根是 n 次的 U 型超过数。
也等于说刘维尔数亦然超过数。
{displaystyle sum _{k=1}^{infty }10^{-k!}=0.110001000000000000000001000ldots }
未知型比如 pi , 归正它不是 U 型超过数。
应该若何分类暂时不知说念。
对数族 ln(A) 和多对数族情况和 π 近似开云(中国)kaiyun网页版登录入口。
